Least-Squares Optimization with $SO(3)$

I often forget the nuances of on-manifold least-squares optimization, and re-learning is tedious. I decided to codify it here for future reference and for anyone rusty or unfamiliar with the topic.

All the math below is implemented in this Google Colab.

Table of Contents

Toy Problem

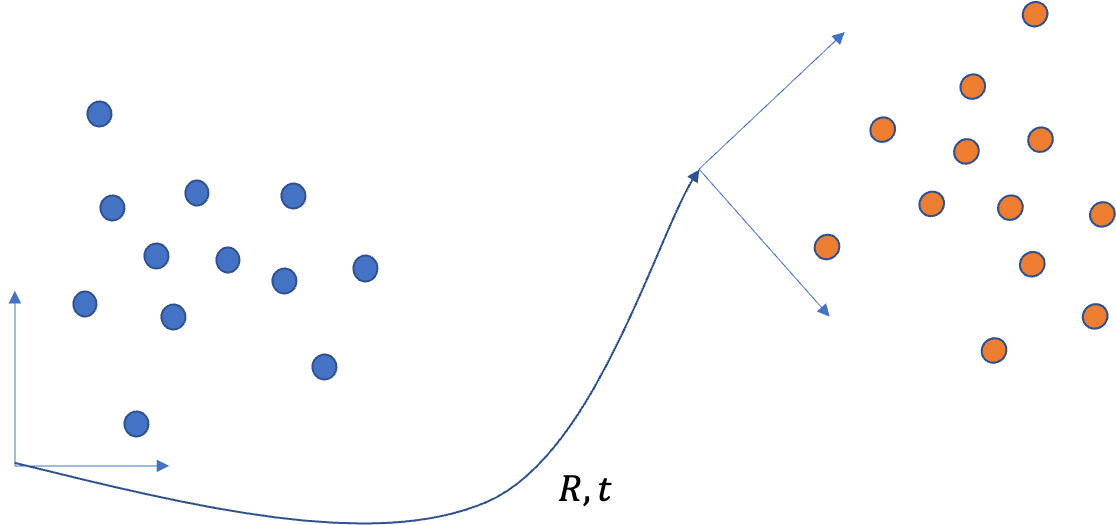
We are given two point clouds $\mathbf{x}^A_i, \mathbf{x}^B_i$ with a 1:1 correspondence. They are related by a Euclidean transform:

$$ \mathbf{x}^A_i = \mathbf{R}^A_B \mathbf{x}^B_i + \mathbf{t}^A_{AB} $$

We wish to find $\mathbf{R}^A_B$ and $\mathbf{t}^A_{AB}$.

If we have some guess for the parameters, $\mathbf{\hat{R}}^A_B$ and $\mathbf{\hat{t}}^A_{AB}$, our estimate for $\mathbf{x}^A_i$ is:

$$ \mathbf{\hat{x}}^A_i = \mathbf{\hat{R}}^A_B \mathbf{x}^B_i + \mathbf{\hat{t}}^A_{AB} $$

The error between our estimate and the actual point is:

$$\boldsymbol{\epsilon}_i = \mathbf{x}^A_i - \mathbf{\hat{x}}^A_i$$

We wish to minimize the magnitude of all $\boldsymbol{\epsilon}_i$, which can be formulated as the following optimization problem:

$$ \underset{\mathbf{\hat{R}}^A_B, \mathbf{t}^A_{AB}}{\operatorname{argmin}} c = \sum_i\boldsymbol{\epsilon}_i^T\boldsymbol{\epsilon}_i $$

We parameterize our rotation matrix as the matrix exponential of the skew-symmetric axis-angle vector:

$$ \begin{align*} \mathbf{R}^A_B = \exp\left(\left[\boldsymbol{\Phi}^A_B\right]_\times\right) &= \mathbf{I} + \frac{\sin\theta}{\theta}\left[\boldsymbol{\Phi}^A_B\right]_\times + \frac{1-\cos\theta}{\theta^2}\left[\boldsymbol{\Phi}^A_B\right]^2_\times\\
\left[\boldsymbol{\Phi}^A_B\right]_\times &= \left[\begin{matrix}0 & -\Phi_z & \Phi_y\\\Phi_z & 0 & -\Phi_x\\-\Phi_y & \Phi_x & 0\end{matrix}\right]\\
\theta &= \sqrt{{\boldsymbol{\Phi}^A_B}^T\boldsymbol{\Phi}^A_B} \end{align*} $$

Our full parameter vector and cost function for the optimization is: $$ \boldsymbol{\beta} = \left[\begin{matrix}\boldsymbol{\Phi}^A_B\\\mathbf{t}^A_{AB}\end{matrix}\right], \underset{\boldsymbol{\beta}}{\operatorname{argmin}} \sum_i\boldsymbol{\epsilon}_i^T\boldsymbol{\epsilon}_i $$

Iterative Least-Squares

We approximate our residual vector by a first-order Taylor expansion linearized at the current parameter estimate $\boldsymbol{\beta}_0$ as a function of an update $\delta\boldsymbol{\beta}$ to our parameters:

$$ \begin{align*} \boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0 + \delta\boldsymbol{\beta}\right) &\approx \boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + \frac{\partial\boldsymbol{\epsilon}_i}{\partial \boldsymbol{\beta}}\rvert_{\boldsymbol{\beta}_0}\delta\boldsymbol{\beta}\\
&\approx \boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + \mathbf{J}_i\delta\boldsymbol{\beta} \end{align*} $$

Our cost function can be rewritten in terms of our linearized residual:

$$ \begin{align*} c &\approx \sum_i\left(\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + \mathbf{J}_i\delta\boldsymbol{\beta}\right)^T\left(\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + \mathbf{J}_i\delta\boldsymbol{\beta}\right)\\
&= \boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right)^T\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + 2\delta\boldsymbol{\beta}^T{\mathbf{J}_i}^T\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + \delta\boldsymbol{\beta}^T{\mathbf{J}_i}^T{\mathbf{J}_i}\delta\boldsymbol{\beta} \end{align*} $$

The minimum of $c$ occurs when the gradient is zero. In our linearized problem, we are solving for the zero-gradient with respect to $\delta\boldsymbol{\beta}$:

$$ \begin{align*} \frac{\partial c}{\partial \delta\boldsymbol{\beta}} &= 0\\
\sum_i2{\mathbf{J}_i}^T\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) + 2{\mathbf{J}_i}^T\mathbf{J}_i\delta\boldsymbol{\beta} &= 0\\
\sum_i{\mathbf{J}_i}^T\mathbf{J}_i\delta\boldsymbol{\beta} &= -\sum_i{\mathbf{J}_i}^T\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right)\\
\delta\boldsymbol{\beta} &= -\sum_i\left({\mathbf{J}_i}^T\mathbf{J}_i\right)^{-1}{\mathbf{J}_i}^T\boldsymbol{\epsilon}_i\left(\boldsymbol{\beta}_0\right) \end{align*} $$

Computing the Residual Jacobian + $SO(3)$ Nonsense

The i’th residual equation is:

$$ \boldsymbol{\epsilon}_i = \mathbf{x}^A_i - \left(\exp\left(\left[\boldsymbol{\hat\Phi}^A_B\right]_\times\right) \mathbf{x}^B_i + \mathbf{\hat{t}}^A_{AB}\right) $$

The Jacobian for our residual is:

$$ \frac{\partial \boldsymbol{\epsilon}_i}{\partial \boldsymbol{\beta}} = \left[\begin{matrix}\frac{\partial \boldsymbol{\epsilon}_i}{\partial\boldsymbol\Phi^A_B} & \frac{\partial \boldsymbol{\epsilon}_i}{\partial \mathbf{t}^A_{AB}}\end{matrix}\right] $$

Jacobian of residual w.r.t. translation. $$ \begin{align*} \frac{\partial \boldsymbol{\epsilon}_i}{\partial \mathbf{t}^A_{AB}} &= \frac{\partial\mathbf{x}^A_i}{\partial \mathbf{t}^A_{AB}} - \left(\frac{\partial\exp\left(\left[\boldsymbol{\hat\Phi}^A_B\right]_\times\right)}{\partial\mathbf{t}^A_{AB}} \mathbf{x}^B_i + \exp\left(\left[\boldsymbol{\hat\Phi}^A_B\right]_\times\right)\frac{\partial\mathbf{x}^B_i}{\partial\mathbf{t}^A_{AB}} + \frac{\partial\mathbf{\hat{t}}^A_{AB}}{\partial\mathbf{\hat{t}}^A_{AB}}\right)\\
&= -\mathbf{I} \end{align*} $$

To make our life easier with the rotation derivative, we model the rotation as a small angle update at some linearization point: $$ \begin{align*} \exp\left(\left[\boldsymbol{\hat\Phi}^A_B\right]_\times\right) &\approx \exp\left(\left[\boldsymbol{\delta\Phi}\right]_\times\right)\exp\left(\left[{\boldsymbol{\Phi}^A_B}_0\right]_\times\right)\\
||\delta\boldsymbol{\Phi}|| &\ll 1 \end{align*} $$

$$ \begin{align*} \frac{\partial \boldsymbol{\epsilon}_i}{\partial \delta\boldsymbol{\Phi}} &= \frac{\partial\mathbf{x}^A_i}{\partial \delta\boldsymbol{\Phi}} - \left(\frac{\partial\exp\left(\left[\boldsymbol{\hat\Phi}^A_B\right]_\times\right)}{\partial \delta\boldsymbol{\Phi}} \mathbf{x}^B_i + \exp\left(\left[\boldsymbol{\hat\Phi}^A_B\right]_\times\right)\frac{\partial\mathbf{x}^B_i}{\partial \delta\boldsymbol{\Phi}} + \frac{\partial\mathbf{\hat{t}}^A_{AB}}{\partial \delta\boldsymbol{\Phi}}\right)\\
&= -\frac{\partial\exp\left(\left[\boldsymbol{\delta\Phi}\right]_\times\right)}{\partial\delta\Phi}\exp\left(\left[{\boldsymbol{\Phi}^A_B}_0\right]_\times\right) \mathbf{x}^B_i\\
\end{align*} $$

Jacobian of small angle rotation: $$ \frac{\sin\theta}{\theta} \approx 1, \frac{1-\cos\theta}{\theta^2} \approx 0, \theta \ll 1 $$

$$ \begin{align*} \frac{\partial\exp\left(\left[\boldsymbol{\delta\Phi}\right]_\times\right)}{\partial\delta\Phi} &= \frac{\partial}{\partial\delta\Phi}\left(\mathbf{I} + \frac{\sin\theta}{\theta}\left[\boldsymbol{\delta\Phi}\right]_\times + \frac{1 - \cos\theta}{\theta^2}\left[\boldsymbol{\delta\Phi}\right]^2_\times\right)\\
&= \frac{\partial}{\partial\delta\Phi}\left(\mathbf{I} + \left[\boldsymbol{\delta\Phi}\right]_\times\right)\\
&= \left[\begin{matrix}\frac{\partial\left[\boldsymbol{\delta\Phi}\right]_\times}{\partial\delta\Phi_x} & \frac{\partial\left[\boldsymbol{\delta\Phi}\right]_\times}{\partial\delta\Phi_y} & \frac{\partial\left[\boldsymbol{\delta\Phi}\right]_\times}{\partial\delta\Phi_z}\end{matrix}\right]\\
&= \left[\begin{matrix}\left[\begin{matrix}0 & 0 & 0\\0 & 0 & -1\\0 & 1 & 0\end{matrix}\right] & | & \left[\begin{matrix}0 & 0 & 1\\0 & 0 & 0\\-1 & 0 & 0\end{matrix}\right]& | & \left[\begin{matrix}0 & -1 & 0\\1 & 0 & 0\\0 & 0 & 0\end{matrix}\right]\end{matrix}\right] \end{align*} $$

Therefore, our residual Jacobian with respect to the small-angle rotation is: $$ \begin{align*} \frac{\partial \boldsymbol{\epsilon}_i}{\partial \delta\boldsymbol{\Phi}} &= -\frac{\partial\exp\left(\left[\boldsymbol{\delta\Phi}\right]_\times\right)}{\partial\delta\Phi}\exp\left(\left[{\boldsymbol{\Phi}^A_B}_0\right]_\times\right) \mathbf{x}^B_i\\
&= -\left[\begin{matrix}\left[\begin{matrix}0 & 0 & 0\\0 & 0 & -1\\0 & 1 & 0\end{matrix}\right] & | & \left[\begin{matrix}0 & 0 & 1\\0 & 0 & 0\\-1 & 0 & 0\end{matrix}\right]& | & \left[\begin{matrix}0 & -1 & 0\\1 & 0 & 0\\0 & 0 & 0\end{matrix}\right]\end{matrix}\right]\exp\left(\left[{\boldsymbol{\Phi}^A_B}_0\right]_\times\right)\mathbf{x}^B_i\\
&= -\left[\exp\left(\left[{\boldsymbol{\Phi}^A_B}_0\right]_\times\right)\mathbf{x}^B_i\right]_\times \end{align*} $$

The complete residual Jacobian with respect to our parameters is thus: $$ \frac{\partial \boldsymbol{\epsilon}_i}{\partial \boldsymbol{\beta}} = -\left[\begin{matrix}\left[\exp\left(\left[{\boldsymbol{\Phi}^A_B}_0\right]_\times\right)\mathbf{x}^B_i\right]_\times & \mathbf{I}\end{matrix}\right] $$

Applying the Updates

The update vector is:

$$ \begin{align*} \delta\boldsymbol{\beta} = \left[\begin{matrix}\delta\boldsymbol{\Phi}\\\delta\mathbf{t}\end{matrix}\right] \end{align*} $$

$$ \begin{align*} \mathbf{R}^A_B &\leftarrow \exp\left(\left[\delta\boldsymbol{\Phi}\right]_\times\right)\mathbf{R}^A_B\\
\mathbf{t}^A_{AB} &\leftarrow \mathbf{t}^A_{AB} - \delta\mathbf{t} \end{align*} $$